News
For many species of insects, wings are like fingerprints – no two patterns are the same. These insects, like many other organisms from leopards to zebrafish, benefit from nature’s seemingly endless ability to generate diverse shapes and patterns. But how do these patterns form?
Researchers from Harvard University have developed a model that can recreate, with only a few parameters, the wing patterns of a large group of insects, shedding light on how these complex patterns form.
The research is published in PNAS.
“We have developed a simple model, with only a few assumptions about how wings grow, that can recapitulate patterns that look close to life-like and can do so for species that are distantly related to each other, from grasshoppers to dragonflies, damselflies and lacewings,” said Christopher Rycroft, Associate Professor of Applied Mathematics at the Harvard John A. Paulson School of Engineering and Applied Sciences and senior author of the paper. “This model could be useful for studying the evolution of wing structure and other patterned shapes.”
While the shape and pattern of insect wings vary tremendously across species, nearly all insect wings have veins — thick, strut-like structures embedded on the wing surface. Some insects, such as the well-studied fruit fly, only have a few, large primary veins. The position and shape of these veins are shared between left and right wings of the same individual and among individuals of the same species.
The wing of a fruit fly has only a few, large primary veins. The position and shape of these veins are shared between left and right wings of the same individual and among individuals of the same species. (Wikicommons)
But other insects, such as dragonflies, have a complex network of secondary veins that crisscross the entire wing, partitioning the wing into hundreds or thousands of small, simple shapes. The shape and position of these secondary veins are endlessly variable, generating unique patterns on each individual wing.
These patterns have fascinated biologists and artists for centuries. Leonardo di Vinci, famously inspired by dragonfly flight, sketched dragonfly wings in the early 1500s. Dutch biologist Jan Swammerdam made extraordinarily detailed illustrations of wing patterns in his research on insect development in the mid-1600s. Since then, naturalists and biologists have continued to carefully document insect wings as a basic step in describing and identifying different species.
The researchers drew on this deep well of data to compile a large database of wing specimens.
Wing of the damselfly Hetaerina americana, with polygonized vein domains colored by their circularity. (Image courtesy of Seth Donoughe and Jordan Hoffmann/Harvard University)
Kathy Li, B.A. ‘16, co-author of the paper, began the project as her undergraduate thesis. She collected more than 500 specimens of dragonflies and damselflies from 215 different species, including representatives from 17 families.
She compiled specimens from Harvard entomology classes, illustrations from 20th century reference books, and existing entomological databases. Li separated the wings from the bodies and imaged them to produce 2D images – not exactly what she imagined herself doing as an applied math major.
“I was always interested in biology, so the interdisciplinary aspect of the project was really exciting,” said Li, who is currently pursuing her Ph.D. in applied math at Columbia University. “I like the idea of being able to look at something and connect its geometry to a conclusion about biology.”
Once the database was compiled, the researchers differentiated, or segmented, each individual polygonal shape made from the intersecting veins.
A differentiated, or segmented, wing outlining each individual polygonal shape made from the intersecting veins. (Image courtesy of Jordan Hoffmann and Seth Donoughe/Harvard University).
“We wanted to take this complex shape and turn it into something simpler so we could ask specific questions and compare its geometry across species,” said Jordan Hoffmann, co-author of the paper and Ph.D. candidate at SEAS. “We looked at the geometric properties of these individual shapes, which we called domains. We looked at how elongated each domain was, how many sides it had, how it touched its neighbors.”
Hoffmann and the team found that a lot of the variation in geometry could be described by the size of the domain and its circularity. They also found that while each wing’s pattern is unique, the distribution of domain shapes is strikingly similar across families and species. For example, the size of the domains tends to decrease as they move away from the body, while the shape of the domains tends to become more circular towards the trailing edge of the wing.
“This is like geometric natural history, in which we are looking at how these shapes are distributed across many species,” said Seth Donoughe, co-author of the paper and postdoctoral fellow at the University of Chicago. “Once we had a good way to assess the similarity of wings, we built a simplified model for the development of wing veins.”
The researchers proposed that an unknown inhibitory signal diffuses from multiple signaling centers in the regions between the primary veins. These inhibitory zones emerge randomly and repel one another, and then prevent secondary veins from growing in certain areas. As the wing grows and stretches during development, those zones could form the complex geometries of the wing as the veins grew around them.
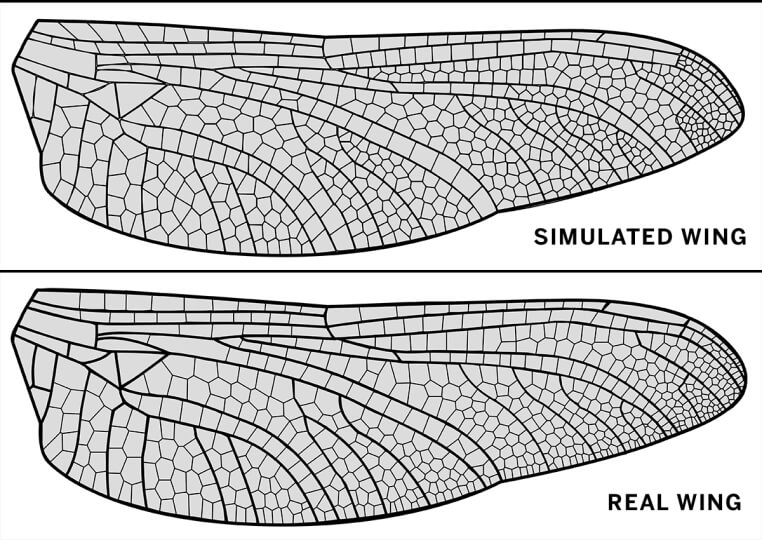
The researchers tested the model on many different insect species — including distantly related insects — and generated life-like reproductions of wings.
“If we’re not careful, even we are sometimes fooled by the simulated wings,” said Donoughe.
A visualization of a real hindwing of the dragonfly Dromogomphus spinosus and a a simulation of the veins for the same wing. (Image courtesy of Jordan Hoffmann and Seth Donoughe/Harvard University).
“The overall approach could be applied to natural patterns that have delighted us for ages, especially in this age where information from many different sources is readily accessible,” said Hoffman. “Problems like these are an exciting springboard for successful collaborations between biology and math.”
This research was co-authored by Mary Salcedo. It was supported by a U.S. Department of Energy (DOE) Computational Science Graduate Fellowship, U.S. National Science Foundation Graduate Training Fellowships, and the Applied Mathematics Program of the U.S. DOE Office of Advanced Scientific Computing Research, the NSF-Simons Center for Mathematical and Statistical Analysis of Biology at Harvard University, and the Harvard Quantitative Biology Initiative.
Topics: Applied Mathematics, Environment
Cutting-edge science delivered direct to your inbox.
Join the Harvard SEAS mailing list.
Scientist Profiles
Christopher Rycroft
Associate in Materials Science and Mechanical Engineering
Press Contact
Leah Burrows | 617-496-1351 | lburrows@seas.harvard.edu