News
SEAS researchers found that different drugs target different stages of protein aggregation and the timing of their administration plays a critical role in inhibiting fibril growth. (Image courtesy of Canva)
Protein aggregation — in which misfolded proteins clump together to form large fibrils — has been implicated in many diseases including Alzheimer’s, Parkinson’s, and type II diabetes. While the exact role these fibrils play in diseases isn’t fully understood, many of the current treatments for diseases like Alzheimer’s and Parkinson’s target the aggregation process. However, finding the right treatment protocols for these drugs, which can be toxic in large doses, is challenging.
Recently, researchers from the Harvard John A. Paulson School of Engineering and Applied Sciences (SEAS) developed a model to better understand how drugs inhibit the growth of protein fibrils, offering a guide to develop more effective strategies to target protein aggregation diseases. The researchers found that different drugs target different stages of protein aggregation and the timing of their administration plays a critical role in inhibiting fibril growth.
“Our research highlights the importance of understanding the relationship between the chemical kinetics of protein misfolding, the mechanisms by which drugs inhibit protein aggregation, and the timing of their administration,” said L Mahadevan, the Lola England de Valpine Professor of Applied Mathematics, of Organismic and Evolutionary Biology, and of Physics at Harvard University. “This understanding could have important implications for intervention protocols to prevent pathological protein aggregation.”
Protein aggregation involves a number of steps, beginning with what’s called primary nucleation, in which the misfolded proteins join together to form a fibril, which then elongates. Once a critical number of fibrils is formed, aggregation accelerates due to a process known as secondary nucleation, leading to exponential growth. The first step associated with the formation of the fibrils is very slow, typically taking several decades, which could explain why Alzheimer's often affects people in their old age. However, once those first fibrils are formed, the disease can progress very rapidly.
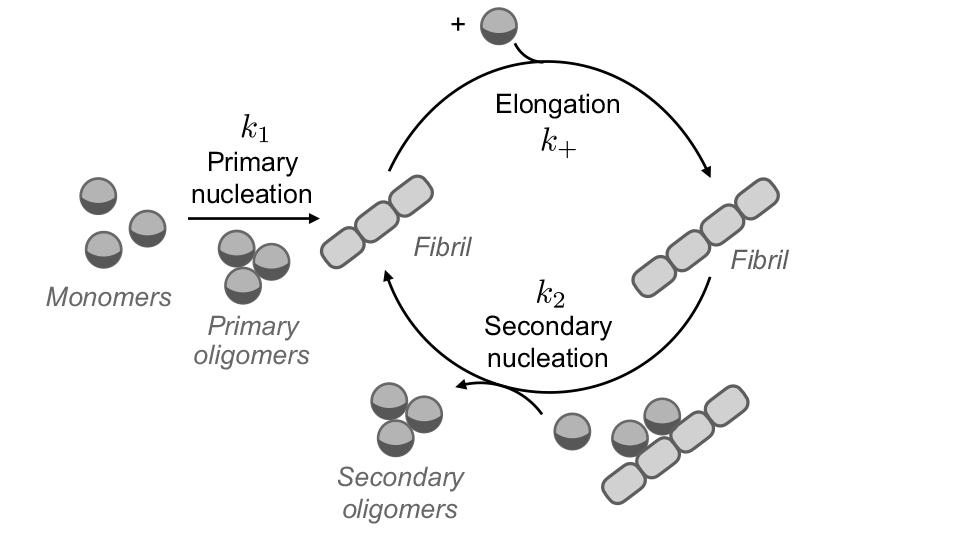
Illustration of protein aggregation. Aggregates are formed through an initial primary nucleation step followed by elongation. Once a critical concentration of aggregates is reached, secondary nucleation introduces a positive feedback cycle leading to exponential growth of aggregate concentration. (Illustration courtesy of L Mahadevan/Harvard SEAS)
Using mathematical methods from control theory, combined with the physics of protein aggregation, the researchers made theoretical predictions on how and when to intervene using drugs.
To test their results, the researchers looked at previously published data on the efficacy of drugs in a model organism, the round worm, C. elegans, where one can trigger the formation of Amyloid b, a misfolded protein associated with Alzheimer’s disease. Its treatment is carried out using two compounds that inhibit the formation of Amyloid b: Bexarotene and DesAb29-35.
The researchers found that drug efficacy depends on whether the compound inhibits primary nucleation or secondary nucleation. Bexarotene, for example, selectively inhibits the primary nucleation that happens early in the disease while DesAb29-36 inhibits secondary nucleation that happens later.
In the absence of drugs, Amyloid-b aggregation causes paralysis in the worms. When Bexarotene was given at the onset of the disease in the larval stages, published data shows that there was a significant recovery of the worm’s mobility. The data also showed that DesAb29-36 was more effective when administered later in the disease’s progression.
“By combining well-known concepts from two different fields, the kinetics of protein aggregation, and optimal control theory, we linked molecular-scale phenomena to macroscale strategies with relevance for a real, practical problem,” said Mahadevan.
“Our approach, which draws on a detailed understanding of the aggregation process and uses this understanding to design rationally potential strategies, is unique,” said Thomas C. T. Michaels, a postdoctoral fellow at Harvard and co-first author of the study along with Christoph Weber, who was a postdoctoral fellow at Harvard and is now a junior group leader at the Max Planck Institute for Complex Physical Systems in Dresden, Germany. “It will allow people to test the efficacy of different compounds against aggregation under optimal conditions at the drug discovery and drug screening level. From these optimal conditions, one could then extrapolate optimal conditions for a trial. So, in this sense, our work could help seed potential trials.”
The research was published in the Proceedings of the National Academy of Sciences. It was supported by the Swiss National Science foundation and the German Research Foundation.
Topics: Applied Mathematics, Health / Medicine
Cutting-edge science delivered direct to your inbox.
Join the Harvard SEAS mailing list.
Press Contact
Leah Burrows | 617-496-1351 | lburrows@seas.harvard.edu